Finite Automata with Thundax P-Zaggy part I
I have moved forward the development of Thundax P-Zaggy with the addition of a Finite Automata builder and simulator. "A deterministic finite automaton (DFA) also known as deterministic finite state machine is a finite state machine that accepts/rejects finite strings of symbols and only produces a unique computation (or run) of the automaton for each input string. (wikipedia)". Building the automata with P-Zaggy is quite simple, so let's start by building a DFA for the following language:
L = {ba | abna, n > 0}.
As it is shown in the previous image, the DFA would be as follows:
With the tool we would be able to create our diagrams placing the states and transitions. Once the diagram is set up, all transitions need to have the transition string to change the ongoing state and initial and final states need to be selected (using right click and selecting "Mark as Start Node" for Initial state and "Mark as End Node" for Final state).
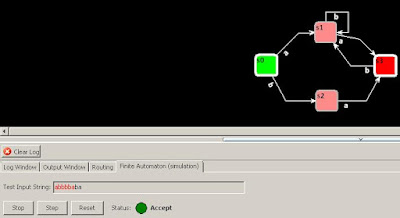
We can start the simulation with very simple steps. Firstly, select the tab called "Finite Automaton (simulation)" and enter the test input string to test. Then press start button to internally initialize the graph as a DFA and press step to process every character of the input string while the diagram is changing states and showing you which is the actual state and whether the string is being accepted or rejected. To set up a single loop transition, select the node and with right click select "Set connector loop" and add text for the transition.
In this beta version, we can also use Regular Expressions in our transitions thanks to the widespread use of regular expressions inside Delphi XE.
From the same screen we can test our regular expressions and check whether if they match or not. There are still some issues to tackle like "empty string" and other considerations that I would be delving into detail in the following days. I am also working on a Layered-Tree-Draw Algorithm using Reingold-Tilford Algorithm and the enhancement of the better recognition of more complex regular expressions.
Have a look at this preview of the functioning of the graph, it is really worth it:
Stay tuned and give P-Zaggy a try from here:
- Thundax P-Zaggy v1.2.0 build 155. (there are two examples included).
Comments
Post a Comment