Raspberry Pi 3 Cluster Test

The following article describes a simple test that was executed on a 4 node (1 controller + 3 workers), Raspberry Pi cluster. The purpose is to obtain reproducible measures of MPI performance that can be useful to MPI developers.  If you haven't read my article about building a Raspberry Pi 3 cluster for parallel programming, you can find it here. The test is a matrix multiplication where each node will perform the calculations of a slice of it and send the results back to the main node. The test will play with 2 main variables: a) the size of the matrix and b) the number of nodes to use to perform the calculations. This should give us the time for each calculation and the speedup.

If you haven't seen my cluster yet, here is an image:

Test Description

The test consist of the following: 
The application generates two square (NxN) matrices A and B of a variable size and defined via arguments. Matrix B is by default visible to each node so we save time sending the array to each node. Then Matrix A is generated in the master node and sliced into several chunks and sent to each individual node of the cluster. The slicing is calculated in the master node. Once each individual node of the cluster has finalised with its calculations, they send the results back to the master node to combine the results and present the resultant matrix.

The slicing mechanism works as follows:

For the example above, imagine that we have a square matrix of size 6x6. We have 4 nodes in our cluster but only three of them are available for calculations. Node 0 or master is just there to arrange initial calculations, send the values to each node and then gather the results from each individual node and display results.

The architecture is quite simple but very common in these scenarios. The beauty of it is that we can increase the number of nodes in the cluster without having to change a single line of code in the application.

As we have a 6x6 matrix, we need to split that by the number of nodes available in the system. Notice that the size of the matrix needs to be divisible by the number of nodes available in the cluster. In this case we have 6 rows and 3 nodes, so there will be 2 rows of data for each node.

Execution

You can find all the source code and results on my github project:

• https://github.com/JordiCorbilla/mpi4py-examples

In there you will find the source code of matrixmultiplication.py, the shell scripts that I used to run the tests, the logs and excel files that I used to gather all the details from each node.

The first step is to calculate the matrix multiplication using just 1 node and then see what's the speedup by using additional nodes.

The sizes of the matrices for this test are defined below:

• 12x12
• 60x60
• 144x144
• 216x216

Each matrix will be run against 3 nodes and from 1 to 4 cpus on each node. Every cycle of the application runs 10 times and we use the average value for defining our results.

Here are the results for the calculations above against 1 node:

Time is in seconds and we can see that the bigger the matrix, the longer it takes to be multiplied. Remember that the complexity for a matrix multiplication is O(n³). We can easily how the graphic tends to draw a cubic function. Just increasing the size of the matrix by 50% we increased the calculation time by 300%.

Here you can see the calculation that the application performs:
Let's see what happens when we run the same matrices against our cluster:

Matrix multiplication against 3 nodes (1 CPU each):

As expected we've reduced one third the execution time for our calculations.

Let's see what happens when we introduce more CPUs:

Matrix multiplication against 3 nodes (2 CPU each):

Matrix multiplication against 3 nodes (3 CPU each):

Matrix multiplication against 3 nodes (4 CPU each):

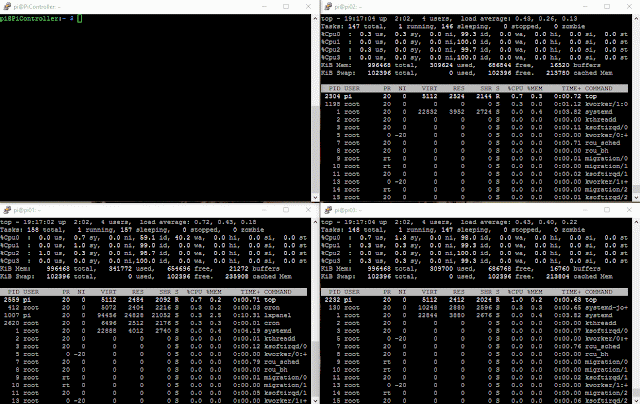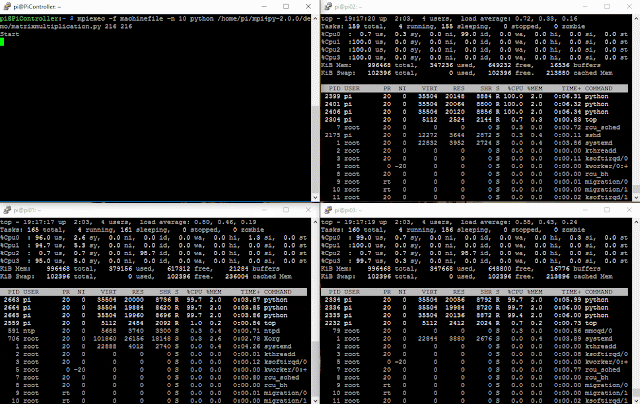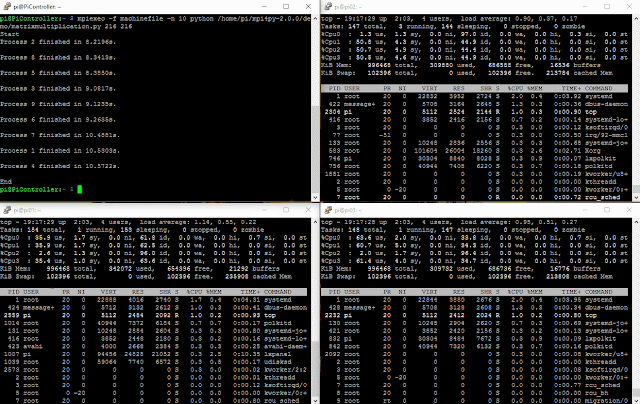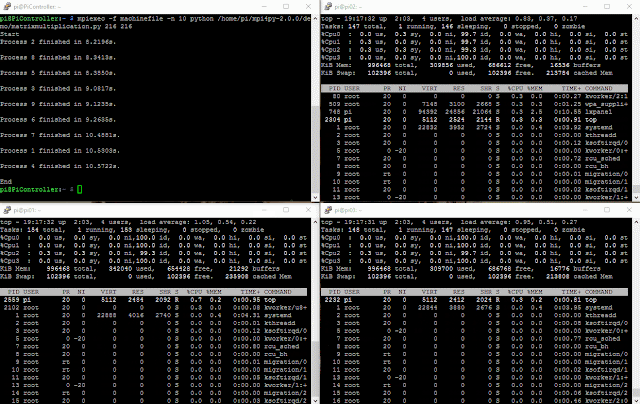
Notice that the RPI3 has 4 CPUs and we can control the number of CPU used through the machinefile and MPI. All the cpus are defined as a node in my machinefile and I made sure that each CPU was working while monitoring them. Below is a graph showing all four cpus working on one of my nodes while running the experiment 216x216 on 12 CPUs:

Here you can see an example running 3 CPUs on each PI. Notice how the CPU's reach 100% on each PI.

Here a sample script to grab the cpu usage for linux:
If we group the graphs together we have:

We can see that the highest throughput is achieved by splitting the matrix using as many nodes as possible and return the results back. Notice that time is not linear in this case as we would suppose to go down to 4s of calculations for each node but we go down to 8s instead (calculation of 216x216 against 12 cpus). We need to consider also that there is an overhead when running MPI and this needs to be taken into consideration. In any case the throughput can be seen in the following figure representing the speedup:

Using 4 CPUs per node gives the highest throughput with a speedup of 6.34. Speedup is calculated with the division of the SeqTime/ParaTime. With this configuration we achieve an 85% of time reduction for our calculations, allowing us to perform large calculations under seconds.

There are loads of tests still to perform on the cluster and this is just a simple example as to how to code a simple example into parallel computing. Please see my project on github for more info and reference.

Jordi